Ellisse

In geometria, l'ellisse, dal greco ἔλλειψις (élleipsis), 'difetto' o 'mancanza', in riferimento a una supposta manchevolezza della curva rispetto alla simmetria della circonferenza, è una curva piana ottenuta intersecando un cono con un piano in modo da produrre una curva chiusa.

Affinché la sezione conica produca una curva chiusa l'inclinazione del piano deve essere superiore a quella della generatrice del cono rispetto al suo asse. Per contro, le due sezioni coniche ottenute con piani aventi inclinazione uguale o inferiore a quella della retta generatrice rispetto all'asse del cono danno vita ad altri due tipi di curve che sono aperte e illimitate: la parabola e l'iperbole.

L'eccentricità di un'ellisse è un termine che misura quanto l'ellisse è schiacciata rispetto ai suoi assi: in termini precisi viene definita come il rapporto tra la distanza tra i due fuochi e la lunghezza dell'asse maggiore — un numero compreso tra 0 e 1 (non incluso).

La circonferenza è un caso speciale di ellisse che si ottiene quando l'intersezione viene fatta con un piano ortogonale all'asse del cono, cioè un'ellisse di eccentricità pari a 0.

L'ellisse può essere anche la proiezione verticale su un piano orizzontale di una circonferenza appartenente a un piano inclinato: se il piano inclinato forma un angolo ${\displaystyle \varphi }$ con il piano orizzontale, la proiezione verticale della circonferenza è un'ellisse di eccentricità ${\displaystyle \sin \varphi }$.

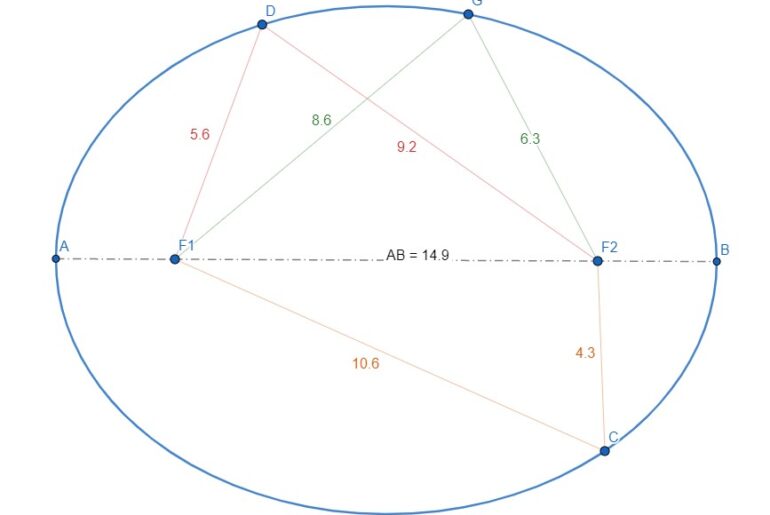
Un'ellisse è anche il luogo geometrico dei punti del piano per i quali la somma delle distanze da due punti fissi detti "fuochi" rimane costante.

Dopo la circonferenza, si tratta della più semplice tra le figure di Lissajous ottenuta dalla composizione dei due moti verticale e orizzontale di tipo sinusoidale della stessa frequenza. In base alle leggi di Keplero, l'orbita di un pianeta è un'ellisse con il Sole che ne occupa uno dei due fuochi.

Elementi di un'ellisse

L'ellisse è una curva che ha l'aspetto di una circonferenza allungata in una direzione: è un esempio di sezione conica e può essere definita come il luogo dei punti del piano per cui la somma delle distanze da due punti fissi, detti fuochi, rimane costante. Se i due fuochi coincidono si ha una circonferenza, che quindi può essere considerata il caso particolare di ellisse a eccentricità nulla.

È una curva con due assi di simmetria e un centro di simmetria. La distanza tra i punti antipodali dell'ellisse, cioè tra punti simmetrici rispetto al suo centro, è massima lungo l'asse maggiore, che contiene anche i due fuochi, ed è minima lungo l'asse minore perpendicolare a quello maggiore. Il semiasse maggiore è una delle due metà dell'asse maggiore: parte dal centro, passa attraverso un fuoco e arriva all'ellisse. Analogamente il semiasse minore è metà dell'asse minore. I due assi sono per l'ellisse l'equivalente del diametro per la circonferenza, mentre i due semiassi sono l'equivalente del raggio.

La dimensione e la forma di un'ellisse sono determinate da due costanti reali positive, dette convenzionalmente ${\displaystyle a}$ e ${\displaystyle b}$. La costante maggiore è la lunghezza del semiasse maggiore mentre la costante minore quella del semiasse minore.

Equazioni

L'equazione dell'ellisse si trova uguagliando la somma delle distanze fra i due fuochi ${\displaystyle F_{1}(x_{1},y_{1})}$ e ${\displaystyle F_{2}(x_{2},y_{2})}$ e un punto generico ${\displaystyle P(x,y)}$ con il doppio del semiasse maggiore:

${\displaystyle {\overline {PF_{1}}} {\overline {PF_{2}}}=2a,}$

che equivale a:

${\displaystyle {\sqrt {(x-x_{1})^{2} (y-y_{1})^{2}}} {\sqrt {(x-x_{2})^{2} (y-y_{2})^{2}}}=2a.}$

In tale equazione, per ottenere un'ellisse non degenere occorre richiedere che ${\displaystyle 2a>d(F_{1},F_{2})}$; se ${\displaystyle 2a=d(F_{1},F_{2})}$ si ottiene il segmento ${\displaystyle F_{1}F_{2}}$.

Per trovare l'equazione "canonica" (o "normale") dell'ellisse, con centro nell'origine e fuochi sull'asse delle ${\displaystyle x}$ (cioè ${\displaystyle a>b}$), si operino le sostituzioni ${\displaystyle y_{1}=0}$, ${\displaystyle y_{2}=0}$, ${\displaystyle x_{1}=-c}$, ${\displaystyle x_{2}=c}$, ${\displaystyle c={\sqrt {a^{2}-b^{2}}}}$. Dopo alcuni passaggi si ricava che l'ellisse centrata nell'origine di un sistema di assi cartesiani con l'asse maggiore posto lungo l'asse delle ascisse è definita dall'equazione:

${\displaystyle {\frac {x^{2}}{a^{2}}} {\frac {y^{2}}{b^{2}}}=1.}$

Con questo riferimento i fuochi hanno coordinate ${\displaystyle F_{1}=(-c,0)}$ ed ${\displaystyle F_{2}=(c,0)}$. La stessa ellisse è rappresentata anche dall'equazione parametrica:

${\displaystyle {\begin{cases}x=a\cos t\\y=b\sin t\\0\leq t<2\pi \end{cases}}}$

che fa uso delle funzioni trigonometriche seno e coseno.

Eccentricità

L'eccentricità ${\displaystyle e}$ di un'ellisse è compresa tra ${\displaystyle 0}$ e ${\displaystyle 1}$ ed è il rapporto della distanza tra i due fuochi ${\displaystyle F_{1}=(-c,0)}$ ed ${\displaystyle F_{2}=(c,0)}$ e la lunghezza dell'asse maggiore ${\displaystyle 2a}$:

${\displaystyle e={\frac {c}{a}}={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}.}$

L'eccentricità rende conto della forma più o meno schiacciata dell'ellisse: quando è uguale a ${\displaystyle 0}$, i due fuochi coincidono e l'ellisse degenera in una circonferenza di raggio ${\displaystyle a}$. Facendo tendere l'eccentricità a ${\displaystyle 1}$, l'ellisse si schiaccia sempre più e quando assume il valore unitario essa degenera in un segmento lungo ${\displaystyle 2a}$ percorso due volte, quindi il perimetro dell'ellisse è uguale a ${\displaystyle 4a}$.

Semilato retto

Il semilato retto di un'ellisse, solitamente denotato dalla lettera ${\displaystyle l}$, è la distanza tra ciascuno dei fuochi dell'ellisse e i punti sull'ellisse di cui i fuochi sono proiezione ortogonale sull'asse maggiore. È legato ad ${\displaystyle a}$ e ${\displaystyle b}$ dalla formula

${\displaystyle l={\frac {b^{2}}{a}}.}$

Corde e diametri

Come per le altre coniche, anche per l'ellisse vale la proprietà seguente: i punti medi di un fascio di corde parallele sono allineati.

Il segmento che congiunge i punti medi di un fascio di corde parallele prende il nome di diametro dell'ellisse. I punti medi delle corde parallele ad un diametro dell'ellisse costituiscono il diametro coniugato al diametro dato. Due diametri coniugati si intersecano nel centro dell'ellisse. Gli assi di simmetria dell'ellisse sono gli unici diametri coniugati perpendicolari tra loro. La retta tangente ad un'ellisse nell'estremo di un diametro è sempre parallela al diametro coniugato.

Equazione in coordinate polari relative a uno dei fuochi

In coordinate polari, un'ellisse con un fuoco nell'origine e con la coordinata angolare ${\displaystyle \theta }$ misurata a partire dall'asse maggiore è rappresentata dall'equazione:

${\displaystyle r(\theta )={\frac {l}{1-e\cos \theta }},}$

dove ${\displaystyle l}$ denota il semilato retto e la coordinata angolare ${\displaystyle \theta }$ è l'angolo che la retta r passante per ${\displaystyle F_{1}}$ forma con l'asse maggiore (vedere figura a lato).

Se si considera la retta ${\displaystyle r}$ passante per il fuoco ${\displaystyle F_{2}}$ e la coordinata angolare ${\displaystyle \theta }$ è l'angolo che la retta ${\displaystyle r}$ passante per ${\displaystyle F_{2}}$ forma con l'asse maggiore, l'equazione diviene:

${\displaystyle r(\theta )={\frac {l}{1 e\cos \theta }}.}$

Area

L'area racchiusa da un'ellisse è data da

${\displaystyle A=\pi ab.}$

Tangente a un'ellisse in un suo punto: formula dello sdoppiamento

L'equazione della retta tangente all'ellisse con centro nell'origine in un suo punto ${\displaystyle P_{0}}$ è:

${\displaystyle {\frac {{xx}_{0}}{a^{2}}} {\frac {{yy}_{0}}{b^{2}}}=1.}$

Il suo coefficiente angolare è dato da:

${\displaystyle m=-{\frac {b^{2}x_{0}}{a^{2}y_{0}}}.}$

Dimostrazione algebrica

Si scriva il seguente sistema non lineare di tre equazioni: la prima è l'equazione dell'ellisse, la seconda impone l'appartenenza all'ellisse del punto ${\displaystyle P_{0}(x_{0},y_{0})}$, la terza impone il passaggio della tangente per il punto ${\displaystyle P_{0}}$ con inclinazione ${\displaystyle m}$ da determinare:

${\displaystyle {\begin{cases}{\dfrac {x^{2}}{a^{2}}} {\dfrac {y^{2}}{b^{2}}}=1\\{\dfrac {x_{0}^{2}}{a^{2}}} {\dfrac {y_{0}^{2}}{b^{2}}}=1\\y-y_{0}=m(x-x_{0})\end{cases}}}$

Nella prima e seconda equazione i secondi membri sono uguali a ${\displaystyle 1}$ e quindi anche i primi membri saranno tra essi uguali:

${\displaystyle {\begin{cases}{\dfrac {x^{2}}{a^{2}}} {\dfrac {y^{2}}{b^{2}}}={\dfrac {x_{0}^{2}}{a^{2}}} {\dfrac {y_{0}^{2}}{b^{2}}}\\y-y_{0}=m(x-x_{0})\end{cases}}}$

${\displaystyle {\begin{cases}{\dfrac {\left(x-x_{0}\right)\left(x x_{0}\right)}{a^{2}}} {\dfrac {\left(y-y_{0}\right)\left(y y_{0}\right)}{b^{2}}}=0\\y-y_{0}=m(x-x_{0}).\end{cases}}}$

Si consideri l'equazione della tangente:

${\displaystyle y-y_{0}=m(x-x_{0}),}$

${\displaystyle y=m(x-x_{0}) y_{0}.}$

Sostituendo nella prima equazione:

${\displaystyle {\begin{cases}{\dfrac {\left(x-x_{0}\right)\left(x x_{0}\right)}{a^{2}}} {\dfrac {\left[m(x-x_{0}\right]\left[m(x-x_{0}) 2y_{0}\right]}{b^{2}}}=0\\y-y_{0}=m(x-x_{0})\end{cases}}}$

${\displaystyle {\begin{cases}{\dfrac {\left(x-x_{0}\right)\left(x x_{0}\right)}{a^{2}}} {\dfrac {m^{2}(x-x_{0})^{2} 2y_{0}m(x-x_{0})}{b^{2}}}=0\\y-y_{0}=m(x-x_{0})\end{cases}}}$

${\displaystyle {\begin{cases}(x-x_{0})\left({\dfrac {\left(x x_{0}\right)}{a^{2}}} {\dfrac {m^{2}(x-x_{0}) 2y_{0}m}{b^{2}}}\right)=0\\y-y_{0}=m(x-x_{0})\end{cases}}}$

Per la legge di annullamento del prodotto:

${\displaystyle x-x_{0}=0,}$

${\displaystyle x=x_{0}.}$

Facilmente verificabile poiché il punto appartiene all'ellisse.

Invece nel secondo fattore:

${\displaystyle {\dfrac {\left(x x_{0}\right)}{a^{2}}} {\dfrac {m^{2}(x-x_{0}) 2y_{0}m}{b^{2}}}=0}$

Poiché ${\displaystyle (x-x_{0})=0}$ e ${\displaystyle x=x_{0}}$:

${\displaystyle {\dfrac {{2x}_{0}}{a^{2}}} {\dfrac {{2y}_{0}m}{b^{2}}}=0}$

${\displaystyle {m=-{\dfrac {b^{2}x_{0}}{a^{2}y_{0}}}}}$ (coefficiente angolare della retta tangente nel punto ${\displaystyle P_{0}}$)

Si sostituisca la pendenza ${\displaystyle m}$ nell'equazione della retta:

${\displaystyle y-y_{0}=-{\dfrac {b^{2}x_{0}}{a^{2}y_{0}}}(x-x_{0})}$

${\displaystyle a^{2}y_{0}y-a^{2}y_{0}^{2}=b^{2}x_{0}^{2}-b^{2}x_{0}x}$

${\displaystyle {{\dfrac {{xx}_{0}}{a^{2}}} {\dfrac {{yy}_{0}}{b^{2}}}={\dfrac {x_{0}^{2}}{a^{2}}} {\dfrac {y_{0}^{2}}{b^{2}}}}.}$

Per ipotesi nel sistema

${\displaystyle {{\dfrac {x_{0}^{2}}{a^{2}}} {\dfrac {y_{0}^{2}}{b^{2}}}=1}.}$

Quindi:

${\displaystyle {{\dfrac {{xx}_{0}}{a^{2}}} {\dfrac {{yy}_{0}}{b^{2}}}=1}.}$

Dimostrazione differenziale

Una dimostrazione alternativa può essere fatta ricorrendo alla derivata della funzione ellisse ${\displaystyle {\frac {x^{2}}{a^{2}}} {\frac {y^{2}}{b^{2}}}=1}$ nel punto ${\displaystyle P_{0}}$: infatti basta ricordare che la derivata di una funzione in un suo punto coincide con il coefficiente angolare della retta tangente nel punto stesso. Effettuando quindi la derivata rispetto a ${\displaystyle x}$ dell'equazione dell'ellisse si ottiene:

${\displaystyle {\frac {2x}{a^{2}}} {\frac {2yy'}{b^{2}}}=0.}$

Poiché ${\displaystyle y'}$ con il coefficiente angolare ${\displaystyle m}$, si ottiene

${\displaystyle m=y'=-{\frac {b^{2}x}{a^{2}y}},}$

che calcolata nel punto ${\displaystyle P_{0}(x_{0},y_{0})}$ fornisce:

${\displaystyle {m=-{\frac {b^{2}x_{0}}{a^{2}y_{0}}}}.}$

Proprietà tangenziale

Una tangente all'ellisse in un suo punto ${\displaystyle P}$ forma angoli uguali con le rette passanti per ${\displaystyle P}$ e per ciascuno dei due fuochi.

Per dimostrare questa proprietà si può ricorrere al teorema di Erone in base al quale data una retta ${\displaystyle r}$ e due punti ${\displaystyle Q}$ ed ${\displaystyle R}$ ad essa esterni, il punto ${\displaystyle P}$ della retta ${\displaystyle r}$ che minimizza la somma ${\displaystyle {\overline {PQ}} {\overline {PR}}}$ è quello per il quale i segmenti ${\displaystyle {\overline {PQ}}}$ e ${\displaystyle {\overline {PR}}}$ formano angoli uguali con la retta ${\displaystyle r}$.

Consideriamo a tale scopo un'ellisse con fuochi ${\displaystyle Q}$ ed ${\displaystyle R}$: un suo qualunque punto ${\displaystyle P}$ soddisfa la condizione

${\displaystyle {\overline {PQ}} {\overline {PR}}=2a.}$

Per un qualunque punto ${\displaystyle S}$ interno all'ellisse vale la condizione

${\displaystyle {\overline {SQ}} {\overline {SR}}<2a.}$

Si consideri ora una retta passante per un punto ${\displaystyle P}$ dell'ellisse tale da formare angoli uguali con i segmenti ${\displaystyle {\overline {PQ}}}$ e ${\displaystyle {\overline {PR}}}$: per il teorema di Erone, il punto ${\displaystyle P}$ è il punto della retta che rende minima la somma ${\displaystyle {\overline {PQ}} {\overline {PR}}}$. Ciò implica che la retta è tangente all'ellisse: infatti se così non fosse la retta entrerebbe dentro l'ellisse e detto ${\displaystyle S}$ un suo punto ad essa interno varrebbe la condizione ${\displaystyle {\overline {SQ}} {\overline {SR}}<2a}$ in contrasto con il teorema di Erone per il quale in ${\displaystyle P}$ e non in ${\displaystyle S}$ si sarebbe dovuta registrare la minima somma. Resta così dimostrata l'affermazione iniziale.

Da questo enunciato segue che in un tavolo da biliardo a forma di ellisse una palla lanciata senza effetto da uno dei due fuochi verrà riflessa dal bordo e passerà necessariamente per l'altro fuoco. La stessa cosa si verificherà in uno specchio concavo a forma di ellisse nel quale tutti i raggi luminosi emessi da uno dei due fuochi passeranno necessariamente per l'altro fuoco indipendentemente dalla direzione seguita: da qui deriva il nome di fuochi dati a questi due particolari punti dell'ellisse. Analogamente, in una camera a forma di ellisse le onde sonore che partono da uno dei due fuochi raggiungeranno l'altro da tutte le direzioni e poiché la distanza percorsa nel tragitto da un fuoco all'altro è sempre la stessa le onde arriveranno tutte sincronizzate: questo spiega perché due persone poste nei due fuochi di una stanza ellittica possono comunicare facilmente anche da lunghe distanze, a differenza di due persone più vicine tra loro ma non situate nei fuochi.

Tangente a un'ellisse passante per un suo punto

Si consideri una ellisse di fuochi ${\displaystyle F_{1}}$, ${\displaystyle F_{1}}$ e asse maggiore ${\displaystyle 2a}$ e un punto ${\displaystyle P}$ appartenente all'ellisse. Esistono due metodi grafici per tracciare la tangente in un punto ${\displaystyle P}$ dell'ellisse.

Primo metodo

Tracciare i segmenti ${\displaystyle PF_{1}}$ e ${\displaystyle PF_{2}}$. Tracciare la bisettrice ${\displaystyle s}$ dell'angolo ${\displaystyle {\widehat {F_{1}PF_{2}}}}$. Tracciare la retta ${\displaystyle t}$ perpendicolare a s nel punto ${\displaystyle P}$. La retta ${\displaystyle t}$ è la retta tangente cercata.

Basta dimostrare che tale retta soddisfa la proprietà tangenziale precedentemente descritta. Infatti gli angoli ${\displaystyle \beta _{2}}$ e ${\displaystyle \beta _{3}}$ sono congruenti in quanto differenza di angoli rispettivamente congruenti: ai due angoli retti sono sottratti gli angoli ${\displaystyle \alpha _{1}}$ e ${\displaystyle \alpha _{2}}$ congruenti per la bisettrice.

Secondo metodo

Tracciare la circonferenza di centro ${\displaystyle F_{1}}$ e raggio ${\displaystyle 2a}$. Tracciare il segmento ${\displaystyle F_{1}P}$ e prolungarlo fino ad incontrare il punto ${\displaystyle E}$ sulla circonferenza. Tracciare ${\displaystyle PF_{2}}$. Tracciare il segmento ${\displaystyle EF_{2}}$. Fissare il punto medio ${\displaystyle M}$ di ${\displaystyle EF_{2}}$. La retta ${\displaystyle t}$ passante per i punti ${\displaystyle M}$ e ${\displaystyle P}$ è la retta tangente cercata.

Infatti è possibile dimostrare che questa retta soddisfa la proprietà tangenziale precedentemente descritta. ${\displaystyle PF_{2}=PE}$ in quanto differenza di segmenti congruenti (${\displaystyle EP PF_{1}=2a}$ e ${\displaystyle PF_{1} PF_{2}=2a}$. Quindi il triangolo ${\displaystyle PEF_{2}}$ è isoscele e la mediana ${\displaystyle PM}$ relativa alla base ${\displaystyle EF_{2}}$ è anche bisettrice e dunque gli angoli ${\displaystyle \beta _{1}}$ e ${\displaystyle \beta _{2}}$ sono congruenti. D'altra parte gli angoli ${\displaystyle \beta _{1}}$ e ${\displaystyle \beta _{3}}$ sono congruenti in quanto opposti al vertice. E quindi ${\displaystyle \beta _{2}}$ e ${\displaystyle \beta _{3}}$ sono congruenti per la proprietà transitiva.

Tangenti a un'ellisse passante per un punto esterno

I coefficienti angolari delle tangenti all'ellisse ${\displaystyle \Gamma }$: ${\displaystyle {\frac {(x-x_{C})^{2}}{a^{2}}} {\frac {(y-y_{C})^{2}}{b^{2}}}=1}$ condotte dal punto ${\displaystyle P(x_{P},y_{P})}$ a essa esterno si ricavano dalla risoluzione della seguente equazione di secondo grado:

${\displaystyle \left(a^{2}-x_{i}^{2}\right)m^{2} 2x_{i}y_{i}m b^{2}-y_{i}^{2}=0,}$

con ${\displaystyle x_{i}=x_{P}-x_{C}}$ e ${\displaystyle y_{i}=y_{P}-y_{C}}$.

Dimostrazione

Si traslano l'ellisse ${\displaystyle \Gamma }$ e il punto ${\displaystyle P}$ di un vettore ${\displaystyle v=(-x_{C},-y_{C})}$, in modo da ottenere l'ellisse ${\displaystyle \Gamma _{i}}$: ${\displaystyle {\frac {x^{2}}{a^{2}}} {\frac {y^{2}}{b^{2}}}=1}$ e il punto ${\displaystyle P_{i}(x_{i},x_{i})}$, con ${\displaystyle x_{i}=x_{P}-x_{C}}$ e ${\displaystyle y_{i}=y_{P}-y_{C}}$. Sapendo che nella traslazione si conserva anche il parallelismo, i coefficienti angolari delle tangenti a ${\displaystyle \Gamma }$ passanti per ${\displaystyle P}$ sono uguali a quelli delle tangenti a ${\displaystyle \Gamma _{i}}$ passanti per il punto ${\displaystyle P_{i}}$. Si scrive il sistema di due equazioni con la prima relativa all'equazione dell'ellisse e la seconda relativa al fascio di rette passanti per il punto ${\displaystyle P_{i}}$

${\displaystyle {\begin{cases}{\dfrac {x^{2}}{a^{2}}} {\dfrac {y^{2}}{b^{2}}}=1\\y-y_{i}=m(x-x_{i})\end{cases}}}$

${\displaystyle {\begin{cases}{\dfrac {x^{2}}{a^{2}}} {\dfrac {y^{2}}{b^{2}}}=1\\y=mx-{mx}_{i} \ y_{i}\end{cases}}}$

${\displaystyle {\dfrac {x^{2}}{a^{2}}} {\dfrac {m^{2}x^{2} m^{2}x_{i}^{2} y_{i}^{2}-2m^{2}x_{i\ }x 2my_{i}x-2mx_{i}y_{i}}{b^{2}}}-1=0}$

${\displaystyle \left({\dfrac {1}{a^{2}}} {\dfrac {m^{2}}{b^{2}}}\right)x^{2} \left(-{\dfrac {2x_{i}m^{2}}{b^{2}}} {\dfrac {2y_{i}m}{b^{2}}}\right)x \left({\dfrac {x_{i}^{2}m^{2}}{b^{2}}}-{\dfrac {2x_{i}y_{i}m}{b^{2}}} {\dfrac {y_{i}^{2}-b^{2}}{b^{2}}}\right)=0.}$

Si impone la condizione di tangenza, ossia che il discriminante ${\displaystyle \Delta }$ sia nullo:

${\displaystyle {\left(-{\dfrac {2x_{i}m^{2}}{b^{2}}} {\dfrac {2y_{i}m}{b^{2}}}\right)}^{2}-4\left({\dfrac {1}{a^{2}}} {\dfrac {m^{2}}{b^{2}}}\right)\left({\dfrac {x_{i}^{2}m^{2}}{b^{2}}}-{\dfrac {2x_{i}y_{i}m}{b^{2}}} {\dfrac {y_{i}^{2}-b^{2}}{b^{2}}}\right)=0}$

${\displaystyle {\cancel {\dfrac {4m^{4}x_{i}^{2}}{b^{4}}}}-{\cancel {\dfrac {8m^{3}x_{i}y_{i}}{b^{4}}}} {\dfrac {4m^{2}y_{i}^{2}}{b^{4}}}-4\left({\dfrac {x_{i}^{2}m^{2}}{a^{2}b^{2}}}-{\dfrac {2x_{i}y_{i}m}{a^{2}b^{2}}} {\dfrac {y_{i}^{2}-b^{2}}{a^{2}b^{2}}} {\cancel {\dfrac {x_{i}^{2}m^{4}}{b^{4}}}}-{\cancel {\dfrac {2x_{i}y_{i}m^{3}}{b^{4}}}} {\dfrac {\left(y_{i}^{2}-b^{2}\right)m^{2}}{b^{4}}}\right)=0}$

${\displaystyle {\dfrac {4y_{i}^{2}m^{2}}{b^{4}}}-{\dfrac {4x_{i}^{2}m^{2}}{a^{2}b^{2}}}-{\dfrac {4\left(y_{i}^{2}-b^{2}\right)m^{2}}{b^{4}}} {\dfrac {8x_{i}y_{i}m}{a^{2}b^{2}}}-{\dfrac {4\left(y_{i}^{2}-b^{2}\right)}{a^{2}b^{2}}}=0}$

${\displaystyle {\cancel {4a^{2}y_{i}^{2}m^{2}}}-4{b^{2}x}_{i}^{2}m^{2}-4a^{2}\left({\cancel {y_{i}^{2}}}-b^{2}\right)m^{2} 8{b^{2}x}_{i}y_{i}m-4b^{2}\left(y_{i}^{2}-b^{2}\right)=0}$

${\displaystyle -x_{i}^{2}m^{2} a^{2}m^{2}\ 2x_{i}y_{i}m-y_{i}^{2} b^{2}=0}$

${\displaystyle \left(a^{2}-x_{i}^{2}\right)m^{2} 2x_{i}y_{i}m b^{2}-y_{i}^{2}=0.}$

Costruzione geometrica delle rette tangenti ad un'ellisse condotte da un punto esterno

È data un'ellisse di fuochi ${\displaystyle F_{1}}$, ${\displaystyle F_{2}}$ e asse maggiore ${\displaystyle 2a}$, e un punto ${\displaystyle P}$ esterno all'ellisse. Esistono due metodi per tracciare le rette tangenti all'ellisse condotte dal punto esterno ${\displaystyle P}$.

Primo metodo

Tracciare la circonferenza di centro ${\displaystyle F_{1}}$ e raggio ${\displaystyle 2a}$. Tracciare la circonferenza di centro ${\displaystyle P}$ e raggio ${\displaystyle PF_{2}}$. Le due circonferenze si intersecano nei punti ${\displaystyle A}$ e ${\displaystyle B}$. Tracciare i segmenti ${\displaystyle F_{1}A}$ e ${\displaystyle F_{1}B}$. Fissare i punti ${\displaystyle T}$ ed ${\displaystyle S}$ di intersezione tra i due segmenti e l'ellisse. Le rette ${\displaystyle PT}$ e ${\displaystyle PS}$ sono le rette tangenti cercate.

Infatti basta dimostrare che tali rette soddisfano la proprietà tangenziale sopra descritta. Anzitutto si osserva che i triangoli ${\displaystyle TAP}$ e ${\displaystyle TF_{2}P}$ sono congruenti perché hanno i tre lati ordinatamente congruenti: ${\displaystyle TP}$ è in comune, ${\displaystyle PA=PF_{2}}$ perché raggi della stessa circonferenza e ${\displaystyle TA=F_{2}T}$ in quanto differenze di segmenti rispettivamente congruenti, infatti ${\displaystyle TF_{1} TF_{2}=2a}$ e ${\displaystyle TF_{1} TA=2a}$. In particolare gli angoli ${\displaystyle {\widehat {ATP}}={\widehat {F_{2}TP}}}$. D'altra parte anche gli angoli ${\displaystyle {\widehat {tTF_{1}}}={\widehat {ATP}}}$ e quindi la proprietà tangenziale è dimostrata.

Secondo metodo

Tracciare la circonferenza di centro ${\displaystyle F_{1}}$ e raggio ${\displaystyle 2a}$. Tracciare la circonferenza di centro ${\displaystyle P}$ e raggio ${\displaystyle PF_{2}}$. Le due circonferenze si intersecano nei punti ${\displaystyle A}$ e ${\displaystyle B}$. Tracciare i segmenti ${\displaystyle F_{2}A}$ e ${\displaystyle F_{2}B}$. Condurre per ${\displaystyle P}$ la retta ${\displaystyle t}$ perpendicolare al segmento ${\displaystyle F_{2}A}$. Condurre per ${\displaystyle P}$ la retta ${\displaystyle s}$ perpendicolare al segmento ${\displaystyle F_{2}B}$. Le rette ${\displaystyle t}$ ed ${\displaystyle s}$ sono le rette tangenti cercate.

Dalla dimostrazione precedente si osserva che ${\displaystyle TP}$ è bisettrice dell'angolo al vertice del triangolo isoscele ${\displaystyle ATF_{2}}$ e quindi è anche altezza.

Equazione generale di un'ellisse

L'equazione generale dell'ellisse avente i fuochi ${\displaystyle F_{1}(x_{F1},y_{F1})}$ ed ${\displaystyle F_{2}(x_{F2},y_{F2})}$ posti in posizione generica sul piano cartesiano e avente il semiasse maggiore denotato con ${\displaystyle a}$ è data da

${\displaystyle Ax^{2} Bxy Cy^{2} Dx Ey F=0}$

dove i parametri ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$, ${\displaystyle D}$, ${\displaystyle E}$ ed ${\displaystyle F}$ sono uguali a

${\displaystyle A=16a^{2}-4(x_{F1}-x_{F2})^{2},}$

${\displaystyle B=-8(x_{F1}-x_{F2})(y_{F1}-y_{F2}),}$

${\displaystyle C=16a^{2}-4(y_{F1}-y_{F2})^{2},}$

${\displaystyle D=4(x_{F1}-x_{F2})(x_{F1}^{2}-x_{F2}^{2} y_{F1}^{2}-y_{F2}^{2})-16a^{2}(x_{F1} x_{F2}),}$

${\displaystyle E=4(y_{F1}-y_{F2})(x_{F1}^{2}-x_{F2}^{2} y_{F1}^{2}-y_{F2}^{2})-16a^{2}(y_{F1} y_{F2}),}$

${\displaystyle F=4(x_{F1}^{2} y_{F1}^{2})(x_{F2}^{2} y_{F2}^{2})-(x_{F1}^{2} x_{F2}^{2} y_{F1}^{2} y_{F2}^{2}-4a^{2})^{2}.}$

Queste equazioni si ricavano dalla definizione metrica di ellisse:

${\displaystyle {\sqrt {(x-x_{F_{1}})^{2} (y-y_{F_{1}})^{2}}} {\sqrt {(x-x_{F_{2}})^{2} (y-y_{F_{2}})^{2}}}=2a}$

Dalla precedente equazione si eliminano le due radici con due elevamenti al quadrato e infine si uguagliano i coefficienti a quelli dell'equazione generale delle coniche.

Lunghezza

La lunghezza dell'ellisse è:

${\displaystyle p=4aE(e),}$

in cui la funzione ${\displaystyle E}$ è l'integrale ellittico completo di seconda specie ed ${\displaystyle e}$ è l'eccentricità.

Sono state proposte numerose formule approssimate per il calcolo della lunghezza dell'ellisse, che differiscono molto per complessità e accuratezza.

Lo sviluppo in serie è:

${\displaystyle p=2\pi a\left[1-\sum _{n=1}^{\infty }\left(\prod _{k=0}^{n-1}{\frac {2k 1}{2(k 1)}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]=2\pi a\left[{1-\left({1 \over 2}\right)^{2}e^{2}-\left({1\cdot 3 \over 2\cdot 4}\right)^{2}{e^{4} \over 3}-\left({1\cdot 3\cdot 5 \over 2\cdot 4\cdot 6}\right)^{2}{e^{6} \over 5}-\dots }\right].}$

Una semplice ma poco raffinata approssimazione per la lunghezza è

${\displaystyle p\approx \pi {\sqrt {2(a^{2} b^{2})}},}$

che fornisce il risultato esatto quando l'ellisse è una circonferenza, cioè per ${\displaystyle a=b}$, mentre dà un risultato approssimato per eccesso negli altri casi. Nel caso limite in cui ${\displaystyle b=0}$ la formula dà ${\displaystyle p\approx 4,44a}$, mentre il valore esatto è ${\displaystyle p=4a}$. La formula è più precisa per ellissi con bassa eccentricità. Utilizzare questa formula equivale ad assumere che l'ellisse abbia la stessa lunghezza di una circonferenza che ha raggio uguale alla media quadratica dei semiassi dell'ellisse.

Un'approssimazione migliore si ottiene con uno sviluppo in serie nel modo seguente: posto ${\displaystyle h={\frac {(a-b)^{2}}{(a b)^{2}}}}$ si ha

${\displaystyle p=\pi (a b)\sum _{n=0}^{\infty }{\binom {\tfrac {1}{2}}{n}}^{2}h^{n}=\pi (a b){\Bigl (}1 {\tfrac {1}{4}}h {\tfrac {1}{64}}h^{2} {\tfrac {1}{256}}h^{3} \ldots {\Bigr )}.}$

Anche in questo caso l'approssimazione è migliore per le ellissi di bassa eccentricità.

Due formule approssimate sono dovute a Ramanujan:

${\displaystyle p\approx \pi \left(3(a b)-{\sqrt {(3a b)(a 3b)}}\right)}$

${\displaystyle p\approx \pi (a b){\biggl (}1 {\frac {3h}{10 {\sqrt {4-3h}}}}{\biggr )}.}$

Entrambe le formule danno il risultato esatto per una circonferenza e, nel caso generale, l'errore delle due formule è dell'ordine di ${\displaystyle h^{3}}$e di ${\displaystyle h^{5}}$, rispettivamente. Nel caso di ellisse degenere in un segmento (${\displaystyle b=0}$, ${\displaystyle h=1}$) la prima dà ${\displaystyle p\approx 3,983a}$, mentre la seconda dà ${\displaystyle p\approx 3,998a}$, quando il risultato esatto è ${\displaystyle p=4a}$.

Metodo della tangente

Fissare i due fuochi ${\displaystyle F_{1}}$ e ${\displaystyle F_{2}}$ e l'asse maggiore di lunghezza ${\displaystyle 2a}$ (con ${\displaystyle 2a>F_{1}F_{2}}$). Costruire una circonferenza di centro ${\displaystyle F_{1}}$ e raggio ${\displaystyle 2a}$. Fissare sulla circonferenza un punto generico ${\displaystyle K}$. Tracciare il raggio ${\displaystyle F_{1}K}$. Tracciare il segmento ${\displaystyle F_{2}K}$ e l'asse di tale segmento (retta perpendicolare al segmento passante per il suo punto medio ${\displaystyle M}$) che interseca ${\displaystyle F_{1}K}$ nel punto ${\displaystyle P}$. Il punto ${\displaystyle P}$ è equidistante da ${\displaystyle F_{2}}$ e da ${\displaystyle K}$ in quanto sta sull'asse del segmento ${\displaystyle F_{2}K}$. Dunque ${\displaystyle PF_{2}=PK}$. D'altra parte ${\displaystyle PF_{1} PK=2a}$ e quindi ${\displaystyle PF_{1} PF_{2}=2a}$. Quindi ${\displaystyle P}$ è un punto dell'ellisse. Questo metodo viene detto della tangente in quanto la retta ${\displaystyle MP}$ è la tangente all'ellisse nel punto ${\displaystyle P}$, infatti gode della proprietà tangenziale, precedentemente descritta.

Metodo del giardiniere

In questo caso sono note le lunghezze dei lati del rettangolo circoscritto all'ellisse. La linea rossa nella figura qui accanto sia la corda utilizzata dal "giardiniere" per tracciare l'ellisse.

Nel film Agorà del 2009 Ipazia, interpretata da Rachel Weisz, studiando l'orbita della Terra attorno al Sole traccia sulla sabbia un'ellisse con il metodo del giardiniere. In alcuni momenti si vede anche un cono di Apollonio.

Note

Voci correlate

• Coordinate ellittiche
• Diametro coniugato
• Ellisse del giardiniere
• Ellisse di Von Mises
• Ellissoide, un'ellisse in tre o più dimensioni.
• Iperbole (geometria)
• Orbita ellittica
• Parabola (geometria)
• Rappresentazione matriciale delle coniche
• Sezione conica
• Sferoide, l'ellissoide ottenuto ruotando un'ellisse attorno al suo asse maggiore o minore.
• Superellisse, una generalizzazione dell'ellisse, è più squadrata.

Altri progetti

• Wikizionario contiene il lemma di dizionario «ellisse»
• Wikimedia Commons contiene immagini o altri file su ellisse

Collegamenti esterni

• (EN) ellipse, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Ellipse, su MathWorld, Wolfram Research.
• Dall'ellisse all'architettura